一、LightGCN [2020]

《LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation》

1. 为减轻网上的信息过载，推荐系统已被广泛部署以执行个性化的信息过滤。推荐系统的核心是预测用户是否会和 item 进行交互，例如点击、评论、购买、以及其它形式的交互。因此，协同过滤（collaborative filtering: CF）仍然是用于个性化推荐的基础（fundamental）任务。其中， CF 专注于利用历史 user-item 交互来实现预测。

   CF 最常见的范式是学习潜在特征（也称为 embedding ）来表示用户和 item ，并基于 embedding 向量进行预测。

   • 矩阵分解是一种早期的此类模型，它直接将 user ID 直接映射到 user embedding。

     后来一些研究发现，利用用户的历史交互作为输入来增强（augmenting）user ID 可以提高 embedding 的质量。例如：

     • SVD++ 展示了用户历史交互在预测用户评分方面的好处。

     • Neural Attentive Item Similarity: NAIS 区分了历史交互中 item 的重要性，并显示了在预测 item ranking 方面的改进。

     从 user-item 交互图（interaction graph）来看，这些改进可以视为来自于用户子图结构（user subgraph structure）（更具体而言，这子图结构就是用户的直接邻居）来改进 embedding learning 。

   • 为了深化高阶邻居子图结构的使用，人们提出了 NGCF 从而为 CF 实现了SOTA 的性能。NGCF 从图卷积网络（Graph Convolution Network: GCN）中汲取灵感，遵循相同的传播（propagation）规则来 refine embedding ：特征变换（feature transformation）、邻域聚合（neighborhood aggregation）、非线性激活（nonlinear activation）。

   尽管 NGCF 已经显示出有希望的结果，但是LightGCN 的作者认为NGCF 的设计相当沉重（heavy）和冗余（burdensome）：很多操作毫无理由地直接从 GCN 继承下来（而并没有对 GCN 进行彻底的理论研究和消融分析）。因此，这些操作不一定对 CF 任务有用。具体而言，GCN 最初是针对属性图（attributed graph）上的节点分类（node classification）任务提出的，其中每个节点都有丰富的属性作为输入特征。而在 CF 的 user-item 交互图中，每个节点（user 或者 item）仅由一个 one-hot ID 来描述，除了作为标识符之外没有任何具体的语义。在这种情况下，给定 ID embedding 作为输入，执行多层非线性特征变换（这是现代神经网络成功的关键）不会带来任何好处，反而会增加模型训练的难度。

   为了验证这一想法（即NGCF 中的这些操作不一定对 CF 任务有用），在论文 《LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation》 中，作者对 NGCF 进行了广泛的消融研究。通过严格的控制实验（在相同的数据集拆分和评估协议上），作者得出结论：从 GCN 继承的两个操作，特征转换和非线性激活，对 NGCF 的有效性（effectiveness）没有贡献。更令人惊讶的是，删除这两个操作会显著提高准确性（accuracy）。这反映了在图神经网络中添加对目标任务无用（useless）操作的问题：不仅没有带来任何好处，反而降低了模型的有效性。

   受到这些经验发现的启发，作者提出了一个名为 LightGCN 的新模型，其中仅包括 GCN 最重要的组件（component）用于协同过滤 ，即：邻域聚合。具体而言：

   • 在将每个用户（item）和 ID embedding 关联之后，模型在 user-item 交互图上传播 embedding 来 refine 这些 embedding 。

   • 然后，模型将不同传播层（propagation layer）学习的 embedding 以加权和的方式聚合，从而获得用于预测的最终 embedding 。

   整个模型简单而优雅，不仅更容易训练，而且比 NGCF 和其它 SOTA 方法（如 Mult-VAE）获得了更好的实验性能。

   总而言之，论文的主要贡献如下：

   • 经验表明：GCN 两种常见设计，特征变换和非线性激活，对协同过滤的有效性没有正面影响。

   • 论文提出了 LightGCN，它通过仅包含 GCN 中最重要的组件进行推荐，从而在很大程度上简化了模型设计。

   • 论文通过遵循相同的实验 setting，在实验中对比了 LightGCN 和 NGCF，并展示了实质性的提升。

     论文还从技术和经验两个角度对 LightGCN 的合理性进行了深入分析。

2. 相关工作：

   • 协同过滤：协同过滤（Collaborative Filtering: CF）是现代推荐系统中的一种流行技术。

     CF 模型的一种常见范式是将用户和 item 参数化为 embedding，并通过重建历史 user-item 交互来学习 embedding 参数。早期的 CF 模型，如矩阵分解（matrix factorization: MF）将用户（或 item ）的 ID 映射到 embedding 向量中。最近的神经推荐模型如 NCF 和 LRML 使用相同的 embedding 组件，但是同时增强了基于神经网络的交互建模（interaction modeling）。

     除了仅使用 ID 信息之外，另一种类型的 CF 方法将历史 item 视为用户已经存在（pre-existing）的特征，从而实现更好的 user representation 。例如，FISM 和 SVD++ 使用历史 item 的 ID embedding 的加权均值作为目标用户的 embedding 。最近，研究人员意识到历史 item 对塑造个人兴趣有不同的贡献。为此，人们引入了注意力机制来捕获不同的贡献，如 ACF 和 NAIS，从而自动学习每个历史 item 的重要性。当以 user-item 二部图的形式重新审视历史交互时，性能的提高可以归因于局部邻域（一阶邻域）的编码，这可以改进 embedding learning 。

     即，将历史 item 视为用户行为特征，这是一种二部图上的局部邻域编码技术。

   • 用于推荐的图方法：另一个相关的研究方向是利用 user-item 图结构进行推荐。

     之前的工作，如 ItemRank，使用标签传播机制（label propagation mechanism）在图上直接传播用户偏好分（user preference score），即鼓励相连的节点具有相似的 label。最近出现的图神经网络（ graph neural network: GNN）揭示了图结构建模，尤其是高阶邻居，从而指导 embedding learning 。

     • 早期的研究定义了谱域（spectral domain）上的图卷积，例如拉普拉斯特征分解（Laplacian eigen-decomposition）（《Spectral Networks and Locally Connected Networks on Graphs 》）和切比雪夫多项式（Chebyshev polynomial）（《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》），但是它们的计算成本很高。

     • 后来，GraphSage 和 GCN 重新定义了空域（spatial domain）中的图卷积，即聚合邻域的 embedding 从而 refine 目标节点的 embedding。由于其可解释性（interpretability） 和效率（efficiency），它们很快成为 GNN 的流行公式并被广泛使用。

     • 受图卷积力量的推动，NGCF、GC-MC、PinSage 等最近的努力使得 GCN 适应于 user-item 交互图，并捕获高阶邻域中的 CF 信号从而进行推荐。

     值得一提的是，最近的一些努力提供了对 GNN 的深入洞察（insight），这激发了我们开发 LightGCN。具体而言，《Simplifying Graph Convolutional Networks》 认为 GCN 不必要的复杂性，通过移除非线性、并将多个权重矩阵融合为一个从而开发简化的 GCN （simplified GCN: SGCN ）模型。LightGCN 和 SGCN 的一个主要区别是：它们是针对不同的任务开发的，因此模型简化的合理性是不同的。具体而言：

     • SGCN 用于节点分类，对模型的可解释性和效率进行了简化。

     • 相比之下，LightGCN 用于协同过滤，其中每个节点只有一个 ID 特征。因此，我们执行简化的理由更充分：非线性和权重矩阵对于 CF 毫无用处，甚至会损害模型训练。

     对于节点分类准确性，SGCN 与 GCN 相当（有时弱于）。对于 CF 准确性，LightGCN 的性能大大优于 GCN （比 NGCF 提高了 15% 以上）。

     最后，同时进行的另一项工作 《Revisiting Graph based Collaborative Filtering: A Linear Residual Graph Convolutional Network Approach》 也发现非线性在 NGCF 中是不必要的，并为 CF 开发了线性 GCN 模型。相比之下，我们的 LightGCN 更进了一步：我们删除了所有冗余参数，仅保留了 ID embedding，使模型像 MF 一样简单。

1.1 模型

1.1.1 NGCF

1. 我们首先介绍 NGCF，这是一个具有代表性的、SOTA 的 GCN 推荐模型。然后我们对 NGCF 进行消融研究，以判断 NGCF 中每个操作的有效性。本节的贡献是表明 GCN 中的两种常见操作，特征转换和非线性激活，对协同过滤没有正面影响。

a. NGCF 介绍

1. 首先每个用户和每个 item 都关联一个 ID embedding。令 ${\overrightarrow{\mathbf{e}}}_u^{(0)}$$\mathbf{\vec e}_u^{(0)}$ 表示用户 $u$$u$ 的 ID embedding、${\overrightarrow{\mathbf{e}}}_i^{(0)}$$\mathbf{\vec e}_i^{(0)}$ 表示item $i$$i$ 的 ID embedding 。NGCF 利用 user-item 交互图来传播 embedding，即：

   $$\begin{array}{c}{\overrightarrow{\mathbf{e}}}_u^{(l+1)}=\sigma ({\mathbf{W}}_1^{(l)}{\overrightarrow{\mathbf{e}}}_u^{(l)}+\sum _{i\in {\mathcal{N}}_u}\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}({\mathbf{W}}_1^{(l)}{\overrightarrow{\mathbf{e}}}_i^{(l)}+{\mathbf{W}}_2^{(l)}({\overrightarrow{\mathbf{e}}}_i^{(l)}\odot {\overrightarrow{\mathbf{e}}}_u^{(l)})))\\ {\overrightarrow{\mathbf{e}}}_i^{(l+1)}=\sigma ({\mathbf{W}}_1^{(l)}{\overrightarrow{\mathbf{e}}}_i^{(l)}+\sum _{u\in {\mathcal{N}}_i}\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}({\mathbf{W}}_1^{(l)}{\overrightarrow{\mathbf{e}}}_u^{(l)}+{\mathbf{W}}_2^{(l)}({\overrightarrow{\mathbf{e}}}_u^{(l)}\odot {\overrightarrow{\mathbf{e}}}_i^{(l)})))\end{array}$$

   其中：

   • ${\overrightarrow{\mathbf{e}}}_u^{(l)},{\overrightarrow{\mathbf{e}}}_i^{(l)}$$\mathbf{\vec e}_u^{(l)},\mathbf{\vec e}_i^{(l)}$ 分别为用户 $u$$u$和 item $i$$i$ 在第 $l$$l$ 层的 refined embedding 。

   • $\sigma (\cdot )$$\sigma(\cdot)$ 为非线性激活函数。

   • ${\mathcal{N}}_u$$\mathcal N_u$ 为用户 $u$$u$ 直接交互的 item 集合，${\mathcal{N}}_i$$\mathcal N_i$ 为与 item $i$$i$ 直接交互的 user 集合。

   • ${\mathbf{W}}_1^{(l)},{\mathbf{W}}_2^{(l)}$$\mathbf W^{(l)}_1,\mathbf W^{(l)}_2$ 为第 $l$$l$ 层可训练的权重矩阵，用于执行特征变换。

   通过传播 $L$$L$ 层，NGCF 得到了 $L+1$$L+1$ 个 embedding $\{{\overrightarrow{\mathbf{e}}}_u^{(0)},{\overrightarrow{\mathbf{e}}}_u^{(1)},\cdots ,{\overrightarrow{\mathbf{e}}}_u^{(L)}\}$$\left\{\mathbf{\vec e}_u^{(0)},\mathbf{\vec e}_u^{(1)},\cdots,\mathbf{\vec e}_u^{(L)}\right\}$来描述一个用户、得到了 $L+1$$L+1$ 个 embedding $\{{\overrightarrow{\mathbf{e}}}_i^{(0)},{\overrightarrow{\mathbf{e}}}_i^{(1)},\cdots ,{\overrightarrow{\mathbf{e}}}_i^{(L)}\}$$\left\{\mathbf{\vec e}_i^{(0)},\mathbf{\vec e}_i^{(1)},\cdots,\mathbf{\vec e}_i^{(L)}\right\}$来描述一个item 。

   然后 NGCF 拼接这 $L+1$$L+1$ 个 embedding 从而获得最终的 user embedding 和 item embedding，并使用内积来生成预估分。

2. NGCF 很大程度上遵循了标准的 GCN，包括使用非线性激活函数 $\sigma (\cdot )$$\sigma(\cdot)$ 和特征变换矩阵 ${\mathbf{W}}_1^{(l)},{\mathbf{W}}_2^{(l)}$$\mathbf W_1^{(l)},\mathbf W_2^{(l)}$ 。然而，我们认为这两种操作对于协同过滤不是太有用。

   • 在半监督节点分类任务中，每个节点都有丰富的语义特征作为输入，例如一篇文章的标题和关键词。因此，执行多层非线性变换有利于特征学习。

   • 然而在协同过滤中， user-item 交互图的每个节点只有一个id 作为输入，没有具体的语义。在这种情况下，执行多层非线性变换无助于学习更好的特征。

     更糟糕的是，执行多层非线性可能会增加训练的难度。接下来我们将提供实验的证据。

b. NGCF 实验探索

1. 我们对 NGCF 进行消融研究，从而探索非线性激活和特征变换的影响。我们使用 NGCF 作者发布的代码，在相同的数据集拆分和评估协议上运行实验，以保持尽可能公平地比较。

2. 由于 GCN 的核心是通过传播来 refine embedding，因此我们对相同 embedding size 下的 embedding 质量更感兴趣。因此，我们将获得最终 embedding 的方式从拼接（即 ${\overrightarrow{\mathbf{e}}}_u^{\ast }={\overrightarrow{\mathbf{e}}}_u^{(0)}||\cdots ||{\overrightarrow{\mathbf{e}}}_u^{(L)}$$\mathbf{\vec e}_u^* =\mathbf{\vec e}_u^{(0)}||\cdots||\mathbf{\vec e}_u^{(L)}$）改为求和（即 ${\overrightarrow{\mathbf{e}}}_u^{\ast }={\overrightarrow{\mathbf{e}}}_u^{(0)}+\cdots +{\overrightarrow{\mathbf{e}}}_u^{(L)}$$\mathbf{\vec e}_u^* =\mathbf{\vec e}_u^{(0)}+\cdots+\mathbf{\vec e}_u^{(L)}$）。注意，这种变更对于 NGCF 的性能影响不大，但是使得以下消融研究更能够表明 GCN 的 refined embedding 质量。

   我们实现了 NGCF 的三个简化的变体：

   • NGCF-f：删除特征变换矩阵 ${\mathbf{W}}_1^{(l)},{\mathbf{W}}_2^{(l)}$$\mathbf W_1^{(l)},\mathbf W_2^{(l)}$ 。

   • NGCF-n：删除非线性激活函数 $\sigma (\cdot )$$\sigma(\cdot)$ 。

   • NGCF-fn：同时删除特征变换矩阵和非线性激活函数。

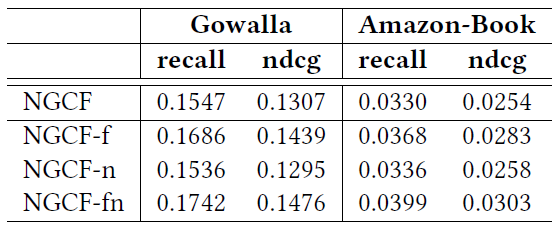
   对于这三个变体，我们保持所有超参数（例如学习率、正则化系数、dropout rate 等等）和 NGCF 的最佳配置相同。

   我们在下表中报告了 Gowalla 和 Amazon-Book 数据集上 2-layer setting 的结果。可以看到：

   • 删除特征变换（即 NGCF-f）导致在所有三个数据集上对 NGCF 的持续提升。

   • 相比之下，删除非线性激活函数（即 NGCF-n ）不会对准确性accuracy 产生太大影响。

   • 如果我们同时删除特征变换矩阵和非线性激活函数（即 NGCF-fn），那么性能会得到显著提高。

   根据这些观察，我们得出以下结论：

   • 添加特征变换对 NGCF 产生负面影响，因为在 NGCF 和 NGCF-n 这两个模型中删除特征变换（即 NGCF-f 和 NGCF-fn）显著提高了性能。

   • 添加非线性激活函数在包含特征变换时影响很小（NGCF vs NGCF-n），但是在禁用特征变换时会产生负面影响（NGCF-f vs NGCF-fn）。

   • 总体而言，特征变换和非线性激活函数对 NGCF 产生了相当负面的影响。因为通过同时移除它们，NGCF-fn 表现出比 NGCF 的巨大提升（召回率相对提高 9.57% ）。

   

3. 为了更深入地了解表中获得的分数，以及理解为什么 NGCF 在这两种操作下（特征变换和非线性激活）恶化，我们在下图中绘制了训练损失和测试 recall 。

   可以看到：

   • 在整个训练过程中，NGCF-fn 的训练损失要比 NGCF, NGCF-f, NGCF-n 低得多。

     NGCF-fn 的训练损失和测试的 recall 曲线保持一致，并且这种较低的训练损失成功地转化为更好的推荐准确性。

   • NGCF 和 NGCF-f 之间的比较显式了类似的趋势，只是提升幅度较小。

   

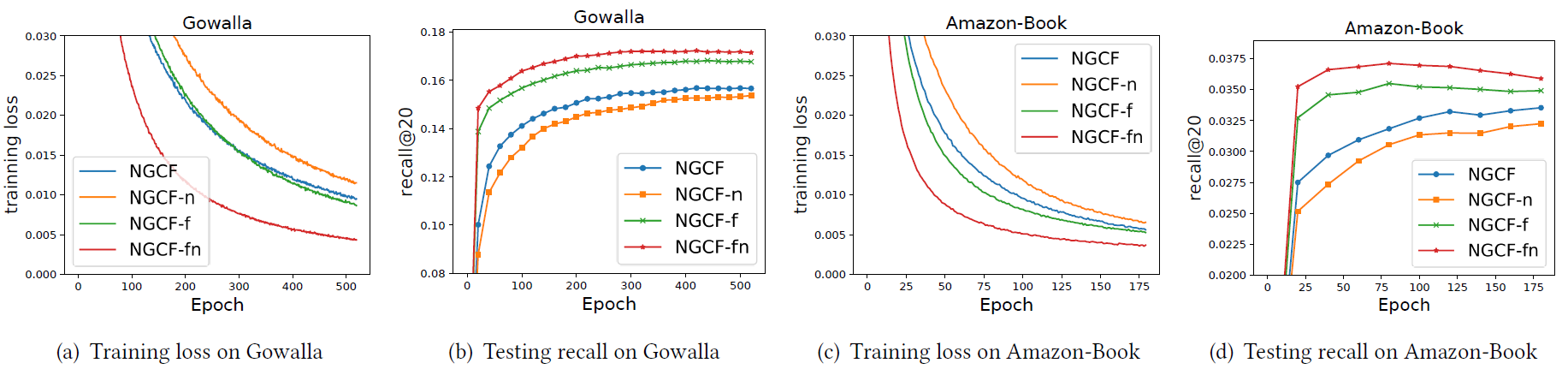
4. 从上述证据中我们可以得出结论：NGCF 的性能恶化源于训练难度，而不是过拟合。

   从理论上讲，NGCF 比 NGCF-f 具有更强的表示能力，因为将权重矩阵 ${\mathbf{W}}_1^{(l)},{\mathbf{W}}_2^{(l)}$$\mathbf W_1^{(l)},\mathbf W_2^{(l)}$ 设置为单位矩阵 $\mathbf{I}$$\mathbf I$ 可以完全恢复 NGCF-f 模型。然而在实践中，NGCF 表现出比 NGCF-f 更高的训练损失和更差的泛化性能。非线性激活的加入进一步加剧了表示能力和泛化性能之间的差异。

   NGCF 相比 NGCF-f 更高的训练损失，这就是训练难度的表现。理论上 NGCF 的模型容量更大，那么训练损失应该更低。假如 NGCF 模型的训练损失更低、但是测试 auc 反而更差，那么就是过拟合的表现。

5. 为了完善这一部分内容，我们主张在设计推荐模型时，进行严格的消融研究以明确每个操作的影响是非常重要的。否则，包含不太有用的操作会使得模型不必要地复杂化、增加模型训练难度、甚至降低模型的有效性。

1.1.2 LightGCN

1. 前述分析表明：NGCF 是一种用于协同过滤的沉重的、冗余的 GCN 模型。在这些发现的推动下，我们设定了一个目标，即通过包含 GCN 最基本的组件进行推荐从而开发一个轻量（light）而有效（effective）的模型。简单的模型具有以下优势：更容易解释、更容易训练和维护、技术上更容易分析模型行为并将其修改为更有效的方向，等等。

   在这一部分，我们首先展示我们设计的 Light Graph Convolution Network: LightGCN 模型，如下图所示。在 LightGCN 中，仅对前一层邻居的 embedding 执行归一化求和（normalized sum） 。所有其它操作，如自连接（ self-connection）、特征转换、非线性激活等等，都被删除。这在很大程度上简化了 GCN 。在 Layer Combination 中，我们对每一层的 embedding 求和以获得最终 representation 。

   然后我们对 LightGCN 进行深入分析，以展示其简单设计背后的合理性。最后我们描述了如何针对推荐来进行模型训练。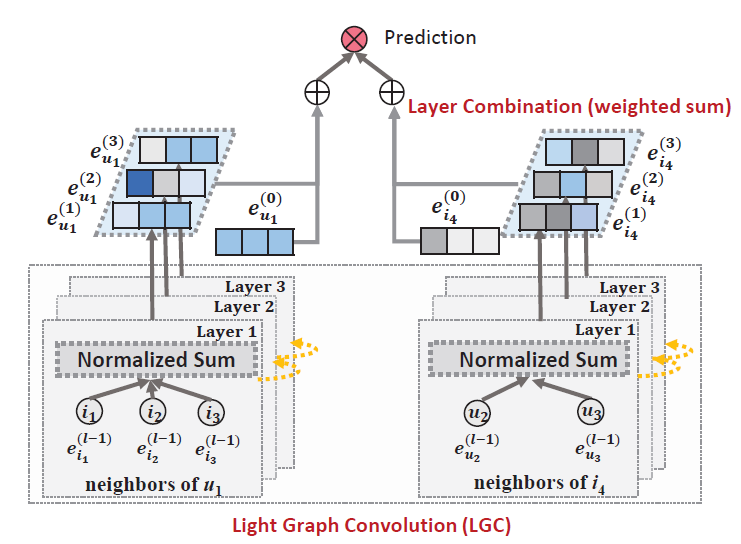

   

a. LightGCN

1. GCN 的基本思想是通过在图上平滑特征来学习节点的 representation。为了实现这一点，它迭代式地执行图卷积（graph convolution），即将邻居的特征聚合为目标节点的新 representation。这种邻域聚合可以抽象为：

   $${\overrightarrow{\mathbf{e}}}_u^{(l+1)}=\text{AGG}({\overrightarrow{\mathbf{e}}}_u^{(l)},\{{\overrightarrow{\mathbf{e}}}_i^{(l)}:i\in {\mathcal{N}}_u\})$$

   其中 $\text{AGG}(\cdot )$$\text{AGG}(\cdot)$ 为一个聚合函数（图卷积的核心），它考虑了目标节点及其邻居节点在第 $l$$l$ 层的 representation。

   很多工作都提出了 $\text{AGG}(\cdot )$$\text{AGG}( \cdot)$，如： GIN 中的 weighted sum 聚合器、GraphSAGE 中的 LSTM 聚合器、BGNN 中的bilinear interaction 聚合器等等。然而，大多数工作都将特征转换或非线性激活与 $\text{AGG}(\cdot )$$\text{AGG}( \cdot)$ 函数联系起来。尽管这些聚合器在具有语义输入特征的节点分类任务或图分类（graph classification）任务上表现良好，但是它们可能对协同过滤造成负担（参考前面的初步分析结果）。

2. Light Graph Convolution: LGC：在 LightGCN 中，我们采用简单的加权和聚合器，删除了特征变换和非线性激活。LightGCN 中的图卷积操作定义为：

   $$\begin{array}{c}{\overrightarrow{\mathbf{e}}}_u^{(l+1)}=\sum _{i\in {\mathcal{N}}_u}\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}{\overrightarrow{\mathbf{e}}}_i^{(l)}\\ {\overrightarrow{\mathbf{e}}}_i^{(l+1)}=\sum _{u\in {\mathcal{N}}_i}\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}{\overrightarrow{\mathbf{e}}}_u^{(l)}\end{array}$$

   对称的归一化项 $\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}$$\frac{1}{\sqrt{|\mathcal N_u||\mathcal N_i|}}$ 遵从标准的 GCN 的设计，这样可以避免 embedding 的幅度（即向量的幅长）随着图卷积运算而增加。这里也可以应用其它选择，如 $L_1$$L_1$ 范数。但是根据经验，我们发现这种对称归一化具有良好的性能（参考后面实验的结果）。

   值得注意的是：在 LGC 中，我们只聚合相连的邻居，没有聚合目标节点本身（即自连接）。这和大多数现有的图卷积操作不同，现有的图卷积通常聚合扩展的邻域（包含节点自身）并需要专门处理自连接。这是因为：层组合操作（layer combination operation）本质上捕获了和自连接相同的效果，因此在 LGC 中没有必要包含自连接。

   关于层组合操作的内容接下来介绍，并且我们还将证明层组合操作和自连接本质上是相同的效果。

3. 层组合和模型预测（Layer Combination and Model Prediction）：在 LightGCN 中，唯一可训练的模型参数是第 0 层的 embedding，即所有用户的 ${\overrightarrow{\mathbf{e}}}_u^{(0)}$$\mathbf{\vec e}_u^{(0)}$ 和所有 item 的 ${\overrightarrow{\mathbf{e}}}_i^{(0)}$$\mathbf{\vec e}_i^{(0)}$。当给定这些embedding 时，可以通过 LGC 计算更高层的 embedding。

   在 $L$$L$ 层 LGC 之后，我们进一步结合在每一层获得的 embedding，从而得到最终的 user representation 和最终的 item representation ：

   $${\overrightarrow{\mathbf{e}}}_u=\sum _{l=0}^L{\alpha }_l{\overrightarrow{\mathbf{e}}}_u^{(l)},{\overrightarrow{\mathbf{e}}}_i=\sum _{l=0}^L{\alpha }_l{\overrightarrow{\mathbf{e}}}_i^{(l)}$$

   其中 ${\alpha }_l\ge 0$$\alpha_l\ge 0$ 表示第 $l$$l$ 层 embedding 在构成final embedding 中的重要性。它可以被视为要手动调优的超参数，也可以被视为要自动优化的模型参数。在我们的实验中，我们发现将 ${\alpha }_l$$\alpha_l$ 统一设为 $1/(L+1)$$1/(L+1)$ 通常会带来良好的性能。因此，我们没有设计特殊的组件来优化 ${\alpha }_l$$\alpha_l$ ，从而避免不必要地复杂化 LightGCN 并保持其简单性。

   和 NGCF 采用多层 embedding 的拼接聚合不同，LightGCN 采用多层 embedding 的加权和聚合。

   我们执行层组合（layer combination）从而获得final representation 的原因有三个：

   • 随着层数的增加，embedding 会过度平滑（over-smooth）。因此，简单地使用最后一层是有问题的。

   • 不同层的 embedding 捕获不同的语义。例如，第一层对有交互的用户和 item 强制执行平滑，第二层平滑与交互item （用户）重叠的用户（item），更高层捕获更高阶的邻近性（proximity）。因此，将它们组合起来将使得representation 更加全面。

   • 将不同层的 embedding 以加权和的方式组合，可以捕捉到带自连接的图卷积的效果，这是 GCN 中的一个重要技巧。

   模型预测被定义user final representation 和 item final representation 的内积：

   $${\hat{y}}_{u,i}={\overrightarrow{\mathbf{e}}}_u^{\mathrm{\top }}{\overrightarrow{\mathbf{e}}}_i$$

4. 矩阵形式：我们提供了 LightGCN 的矩阵形式，以便于实现以及和现有模型的讨论。

   假设 user-item 交互矩阵为 $\mathbf{R}\in {\mathbb{R}}^{M\times N}$$\mathbf R\in \mathbb R^{M\times N}$，其中 $M$$M$ 为用户数量、$N$$N$ 为 item 数量。如果用户 $u$$u$ 和item $i$$i$ 有交互则 $R_{u,i}=1$$R_{u,i}=1$，否则 $R_{u,i}=0$$R_{u,i} = 0$。然后我们得到user-item 交互图的邻接矩阵为：

   $$\begin{array}{c}\mathbf{A}=\left[\begin{array}{cc}\mathbf{0}& \mathbf{R}\\ {\mathbf{R}}^{\mathrm{\top }}& \mathbf{0}\end{array}\right]\end{array}$$

   令第0 层的 embedding 矩阵为 ${\mathbf{E}}^{(0)}\in {\mathbb{R}}^{(M+N)\times d}$$\mathbf E^{(0)}\in \mathbb R^{(M+N)\times d}$，其中 $d$$d$ 为 embedding size。则我们可以得到 LGC 的矩阵等价形式为：

   $${\mathbf{E}}^{(l+1)}=\left({\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}\right){\mathbf{E}}^{(l)}=\tilde{\mathbf{A}}{\mathbf{E}}^{(l)}={\tilde{\mathbf{A}}}^{l+1}{\mathbf{E}}^{(0)}$$

   其中 $\mathbf{D}\in {\mathbb{R}}^{(M+N)\times (M+N)}$$\mathbf D\in \mathbb R^{(M+N)\times (M+N)}$ 是一个对角矩阵（也称度矩阵），$D_{i,i}=\sum _j{A}_{i,j}$$D_{i,i} = \sum_{j} A_{i,j}$ 表示 $\mathbf{A}$$\mathbf A$ 中第 $i$$i$ 行非零元素的个数，$\tilde{\mathbf{A}}={\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$$\tilde {\mathbf A} = \mathbf D^{-1/2}\mathbf A\mathbf D^{-1/2}$ 为对称归一化的矩阵。

   最后，我们得到用于模型预测的final embedding 矩阵为：

   $$\mathbf{E}=\sum _{l=0}^L{\alpha }_l{\mathbf{E}}^{(l)}=\sum _{l=0}^L{\alpha }_l{\tilde{\mathbf{A}}}^l{\mathbf{E}}^{(0)}$$

   .

b. 模型分析

1. 我们进行模型分析以证明 LightGCN 简单设计背后的合理性。

   首先我们讨论了与 Simplified GCN 的联系，这是最近的一个线性 GCN 模型，它将自连接集成到图卷积中。这个分析表明通过层组合，LightGCN 包含了自连接的效果。因此，LightGCN 不需要在邻接矩阵中加入自连接。

   然后我们讨论和 Approximate Personalized Propagation of Neural Predictions: APPNP 的联系，这是最近的一个 GCN 变体，它通过从 Personalized PageRank 的启发来解决过度平滑问题。这个分析表明了 LightGCN 和 APPNP 之间的潜在等效性。因此，我们的 LightGCN 在具有可控过度平滑（controllable oversmoothing）的长距离传播方面享受同样的好处。

   最后，我们分析了第二层 LGC，以展示它如何平滑用户及其二阶邻居。这为 LightGCN 的工作机制提供更多的洞察（insights）。

2. 与 SGCN 的关联：在论文 《Simplifying Graph Convolutional Networks》 中，作者论证了GCN 对节点分类的不必要的复杂性，并提出了 SGCN。SGCN 通过删除非线性并将权重矩阵压缩为一个权重矩阵来简化 GCN。SGCN 中的图卷积定义为：

   $${\mathbf{E}}^{(l+1)}={(\mathbf{D}+\mathbf{I})}^{-1/2}(\mathbf{A}+\mathbf{I}){(\mathbf{D}+\mathbf{I})}^{-1/2}{\mathbf{E}}^{(l)}$$

   其中 $\mathbf{I}$$\mathbf I$ 为单位矩阵，它添加到 $\mathbf{A}$$\mathbf A$ 上从而构成自连接。

   在下面的分析中，为简单起见，我们省略了 $(\mathbf{D}+\mathbf{I}{)}^{-1/2}$$(\mathbf D+\mathbf I)^{-1/2}$ 项，因为该项仅仅对 embedding 执行缩放re-scale 。

   在 SGCN 中，最后一层得到的 embedding 用于下游预测任务，可以表示为：

   $$\begin{array}{c}{\mathbf{E}}^{(L)}=(\mathbf{A}+\mathbf{I}){\mathbf{E}}^{(L-1)}=(\mathbf{A}+\mathbf{I}{)}^L{\mathbf{E}}^{(0)}\\ =C_L^0{\mathbf{E}}^{(0)}+C_L^1\mathbf{A}{\mathbf{E}}^{(0)}+C_L^2{\mathbf{A}}^2{\mathbf{E}}^{(0)}+\cdots +C_L^L{\mathbf{A}}^L{\mathbf{E}}^{(0)}\end{array}$$

   其中 $C_L^l=\frac{L\times \cdots \times (L-l+1)}{l\times \cdots \times 1}$$C_L^l=\frac{L\times\cdots\times (L-l+1)}{l\times\cdots\times 1}$ 表示组合数。

   上述推导表明：将自连接插入到 $\mathbf{A}$$\mathbf A$ 并在其上传播 embedding，本质上等效于在每个 LGC 层传播的 embedding 的加权和。

   添加自连接相当于将每一层的 embedding 向更高层传播，此时最后一层 embedding 隐含了各层的 embedding 信息。这相当于不带自连接的、 LGC 的各层 embedding 的直接聚合。

3. 和 APPNP 的关联：在最近的一项工作 《Predict then propagate: Graph neural networks meet personalized pagerank》 中，作者将 GCN 和Personalized PageRank 联系起来，从中得到启发，并提出一个叫做 APPNP 的 GCN 变体。该变体可以在没有过度平滑（oversmoothing）风险的情况下进行长距离传播。

   受到Personalized PageRank 中的传送设计（teleport design）的启发，APPNP 用起始特征（starting feature）（即第0 层embedding）补充每个传播层，这可以平衡（balance）保留局部性（locality）（即靠近根节点以减轻过度平滑）和利用大的邻域的信息的需要。

   APPNP 中的传播层定义为：

   $${\mathbf{E}}^{(l+1)}=\beta {\mathbf{E}}^{(0)}+(1-\beta )\tilde{\mathbf{A}}{\mathbf{E}}^{(l)}$$

   其中 $\beta$$\beta$ 为传播中控制起始特征保留的 teleport probability ，$\tilde{\mathbf{A}}$$\tilde{\mathbf A}$ 为归一化的邻接矩阵。

   在 APPNP 中，最后一层用于最终预测，即：

   $$\begin{array}{c}{\mathbf{E}}^{(L)}=\beta {\mathbf{E}}^{(0)}+(1-\beta )\tilde{\mathbf{A}}{\mathbf{E}}^{(L-1)}\\ =\beta {\mathbf{E}}^{(0)}+\beta (1-\beta )\tilde{\mathbf{A}}{\mathbf{E}}^{(0)}+(1-\beta {)}^2{\tilde{\mathbf{A}}}^2{\mathbf{E}}^{(L-2)}\\ =\beta {\mathbf{E}}^{(0)}+\beta (1-\beta )\tilde{\mathbf{A}}{\mathbf{E}}^{(0)}+\beta (1-\beta {)}^2{\tilde{\mathbf{A}}}^2{\mathbf{E}}^{(0)}+\cdots +(1-\beta {)}^L{\tilde{\mathbf{A}}}^L{\mathbf{E}}^{(0)}\end{array}$$

   我们可以看到：通过相应的设置 ${\alpha }_l$$\alpha_l$，LightGCN 可以完全恢复 APPNP 使用的预测 embedding 。因此，LightGCN 在对抗过度平滑方面具有 APPNP 的优势：通过适当地设置 $\alpha$$\alpha$，我们允许使用大的 $L$$L$ 进行具有可控过度平滑（controllable oversmoothing）的长程（long-range）建模。

   另一个细微的区别是：APPNP 在邻接矩阵中添加了自连接。然而，正如我们之前所展示的，由于LightGCN 采用了不同层 embedding 的加权和，因此自连接是冗余的。

4. 二阶 embedding 的平滑性：由于 LightGCN 的线性和简单性，我们可以深入了解它如何平滑 embedding。这里我们分析一个两层 LightGCN 来证明其合理性。

   以用户侧为例，直观地，第二层平滑了在交互 item 上有重叠 （overlap） 的所有用户。具体而言，我们有：

   $${\overrightarrow{\mathbf{e}}}_u^{(2)}=\sum _{i\in {\mathcal{N}}_u}\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}{\overrightarrow{\mathbf{e}}}_i^{(1)}=\sum _{i\in {\mathcal{N}}_u}\frac{1}{|{\mathcal{N}}_i|}\sum _{v\in {\mathcal{N}}_i}\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_v|}}{\overrightarrow{\mathbf{e}}}_v^{(0)}$$

   可以看到，如果另一个用户 $v$$v$ 和目标用户 $u$$u$ 有共同的交互 item，那么 $v$$v$ 对 $u$$u$ 的平滑强度（smoothness strength）由以下系数来衡量：

   $$c_{v\to u}=\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_v|}}\sum _{i\in {\mathcal{N}}_u\cap {\mathcal{N}}_v}\frac{1}{|{\mathcal{N}}_i|}$$

   如果 $v$$v$ 和 $u$$u$ 没有共同的交互 item，那么该系数为零。

   这个系数相当容易解释：二阶邻居 $v$$v$ 对 $u$$u$ 的影响由以下因素决定：

   • 共同交互 item 的数量（即：$\sum _{i\in {\mathcal{N}}_u\cap {\mathcal{N}}_v}$$\sum_{i\in \mathcal N_u\cap \mathcal N_v}$ ），数量越多则影响越大。

   • 共同交互item 的流行度（popularity）（即： $|{\mathcal{N}}_i|$$|\mathcal N_i|$），流行度越低（即越能够代表用户的个性化偏好）则影响越大。

   • 用户 $v$$v$ 的活跃度（即：$|{\mathcal{N}}_v|$$|\mathcal N_v|$），越不活跃则影响越大。

   这种可解释性很好地满足了 CF 在度量用户相似性时的假设，并证明了 LightGCN 的合理性。

   由于 LightGCN 公式的对称性，我们可以在 item 方面得到类似的分析。

5. LightGCN 和 SGCN 的一个主要区别在于：LightGCN 和 SGCN 是针对不同的任务开发的，因此模型简化的合理性是不同的。具体而言：SGCN 用于节点分类，对模型的可解释性和效率进行简化。相比之下，LightGCN 用于协同过滤CF，其中每个节点只有一个 ID 特征。因此我们做简化的理由更充分：非线性和权重矩阵对于协同过滤毫无用处，甚至会损害模型训练。

c. 模型训练

1. LightGCN 的可训练参数只是第 0 层的 embedding，即 $\mathrm{\Theta }=\left\{{\mathbf{E}}^{(0)}\right\}$$\Theta=\left\{\mathbf E^{(0)}\right\}$ 。换句话讲，模型复杂度和标准的矩阵分解（matrix factorization: MF）相同。

2. 我们采用贝叶斯个性化排序（Bayesian Personalized Ranking）损失函数。BPR loss 是一种 pairwise loss，它 鼓励观察到的 item 的预测高于未观察到的对应 item ：

   $${\mathcal{L}}_{\text{BPR}}=-\sum _{u=1}^M\sum _{i\in {\mathcal{N}}_u}\sum _{j\ne {\mathcal{N}}_u}\ln \sigma ({\hat{y}}_{u,i}-{\hat{y}}_{u,j})+\lambda {\Vert {\mathbf{E}}^{(0)}\Vert }^2$$

   其中 $\lambda$$\lambda$ 控制了 $L_2$$L_2$ 正则化强度。

   • 我们采用 Adam 优化器，并以 mini-batch 的方式优化。

   • 我们知道其它可能会改进 LightGCN 训练的高级负采样策略，如hard 负采样和对抗采样（adversarial sampling）。我们把这个扩展放在未来，因为它不是这项工作的重点。

3. 注意，我们没有引入 GCN 和 NGCF 中常用的 dropout 机制。原因是我们在 LightGCN 中没有特征变换权重矩阵，因此在 embedding 层上执行 $L_2$$L_2$ 正则化足以防止过拟合。这展示了 LightGCN 简单性的优点：比 NGCF 更容易训练和调优。

   NGCF 需要额外地调优两个 dropout rate（node dropout 和 message dropout），并将每层的 embedding 归一化为单位长度。

4. 还可以学习层的组合系数 $\{{\alpha }_l{\}}_{l=0}^L$$\{\alpha_l\}_{l=0}^L$，或者使用注意力网络对组合系数进行参数化，这在技术上是可行的。即：个性化层的组合系数 ${\alpha }_l$$\alpha_l$ ，以便为不同的用户启用自适应阶次的平滑。例如，稀疏用户可能需要来自高阶邻居的更多信号，而活跃用户则只需要来自低阶邻居的更少信号。

   活跃用户具有大量的一阶 item 邻居，因此使用低阶邻居就可以得到良好的用户 representation ；稀疏用户具有很少的一阶 item 邻居，因此需要高阶邻居来补充从而得到更好的用户 representation 。

   然而，我们发现在训练数据上学习 ${\alpha }_l$$\alpha_l$ 并没有带来改进。这可能是因为训练数据不包含足够的信号来学习可泛化到未知数据的好的 ${\alpha }_l$$\alpha_l$ 。我们还尝试从验证数据中学习 ${\alpha }_l$$\alpha_l$，这是受到 《λOpt: Learn to Regularize Recommender Models in Finer Levels》 的启发，它在验证数据上学习超参数。我们发现性能性能略有提升（小于 1%）。

   我们将探索 ${\alpha }_l$$\alpha_l$ 的最佳设置（如针对不同的用户和 item 来进行个性化）作为未来的工作。

1.2 实验

1. 我们首先描述实验设置，然后和 NGCF 进行详细比较。NGCF 是和 LightGCN 最相关、但是更复杂的方法。接下来我们将 LightGCN 和其它 SOTA 方法进行比较。为了证明 LightGCN 中的设计合理性并揭示其有效的原因，我们进行了消融研究和 embedding 分析。最后我们研究了超参数。

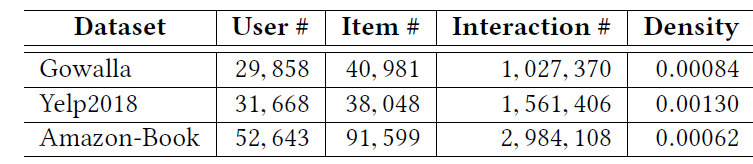
2. 数据集：为了减少实验工作量并保持公平的比较，我们密切遵循 NGCF 工作的配置。我们从 NGCF 作者那里获取了实验数据集（包括训练集、测试集的拆分），其统计数据如下表所示。

   • Gowalla 和 Amazon-Book 和 NGCF 论文中使用的完全一致，因此我们直接使用 NGCF 论文中的结果。

   • 唯一的例外是 Yelp 2018 数据集，这是一个修订版本。根据NGCF作者的说法，之前的版本没有过滤掉测试集中的冷启动item，他们只向我们分享了修订版本。因此，我们在 Yelp 2018 数据集上重新运行了 NGCF。

   • 评估指标是由 all-ranking 协议（用户的所有未交互的 item 都是候选 item ）计算的 recall@20 和 ndcg@20 。

   

3. 对比方法：主要的对比方法是 NGCF，其表现优于多种方法，包括基于 GCN 的模型 GC-MC, PinSage、基于神经网络的模型 NeuMF, CMN、以及基于分解的模型MF, Hop-Rec 。由于比较是在相同评估协议下的相同数据集上进行的，因此我们没有进一步和这些方法进行比较（仅仅比较了 NGCF）。

   我们还进一步比较了两种相关的、且具有竞争力的 CF 方法：

   • Mult-VAE：这是一种基于变分自编码器（variational autoencoder: VAE）的、基于 item 的 CF 方法。它假设数据是从多项式分布中生成的，并使用变分推断（variational inference）进行参数估计。

     我们运行作者发布的代码，并在 [0, 0.2, 0.5] 中调优 dropout rate、在 [0.2, 0.4, 0.6, 0.8] 中调优 $\beta$$\beta$ 。模型架构是原始论文中建议的架构：600 -> 200 -> 600 。

   • GRMF：该方法通过添加图拉普拉斯正则化器（graph Laplacian regularizer）来平滑矩阵分解。为了公平地比较 item 推荐，我们将评分预测损失调整为 BPR loss。

     GRMF 的目标函数为：

     $$\mathcal{L}=-\sum _{u=1}^M\sum _{i\in {\mathcal{N}}_u}(\sum _{j\ne {\mathcal{N}}_u}\ln \sigma ({\overrightarrow{\mathbf{e}}}_u^{\mathrm{\top }}{\overrightarrow{\mathbf{e}}}_i-{\overrightarrow{\mathbf{e}}}_u^{\mathrm{\top }}{\overrightarrow{\mathbf{e}}}_j)+{\lambda }_g{\Vert {\overrightarrow{\mathbf{e}}}_u-{\overrightarrow{\mathbf{e}}}_i\Vert }^2)+\lambda \parallel \mathbf{E}{\parallel }^2$$

     其中 ${\lambda }_g$$\lambda_g$ 在 $[{10}^{-5},{10}^{-4},\cdots ,{10}^{-1}]$$\left[10^{-5},10^{-4},\cdots,10^{-1}\right]$ 之间调优，其它的超参数设置和 LightGCN 相同。

     此外，我们还比较了一个给拉普拉斯图增加归一化的变体：

     $${\lambda }_g{\Vert \frac{{\overrightarrow{\mathbf{e}}}_u}{\sqrt{|{\mathcal{N}}_u|}}-\frac{{\overrightarrow{\mathbf{e}}}_i}{\sqrt{|{\mathcal{N}}_i|}}\Vert }^2$$

     这被称作 GRMF-norm 。这两种 GRMF 方法通过拉普拉斯正则化器在训练中引入 embedding 平滑（测试时还是原始的 embedding 而没有平滑），而我们的 LightGCN 在预测模型中实现了 embedding 平滑。

4. 超参数配置：

   • 与 NGCF 相同，所有模型的 embedding 大小固定为 64，embedding 参数使用 Xavier 方法初始化。

   • 我们使用 Adam 优化器优化 LightGCN，并使用默认的学习率 0.001 和默认的 batch size = 1024 （在 Amazon-Book 上，我们将 batch size 增加到 2048 以提高训练速度）。

   • $L_2$$L_2$ 正则化系数 $\lambda$$\lambda$ 在 $[{10}^{-6},{10}^{-5},\cdots ,{10}^{-2}]$$\left[10^{-6},10^{-5},\cdots,10^{-2}\right]$ 范围内搜索，大多数情况下最优值为 ${10}^{-4}$$10^{-4}$ 。

   • 层组合系数 ${\alpha }_l$$\alpha_l$ 统一设置为 $\frac{1}{1+L}$$\frac{1}{1+L}$ ，其中 $L$$L$ 为层数。

   • 我们在 1 ~ 4 的范围内测试 $L$$L$ ，当 $L=3$$L=3$ 时可以获得令人满意的性能。

   • 早停和验证策略与 NGCF 相同。通常，1000 个 epoch 足以让 LightGCN 收敛。

   我们的实现在 TensorFlow 和 PyTorch 中都可用。

1.2.1 模型比较

1. 与NGCF 比较：我们与 NGCF 进行了详细的比较，下表中记录了不同层（1 层到 4 层）的性能，还显示了每个指标的相对提升比例。其中NGCF 在 Gowalla 和 Amazon-Book 上的结果来自于 NGCF 原始论文。

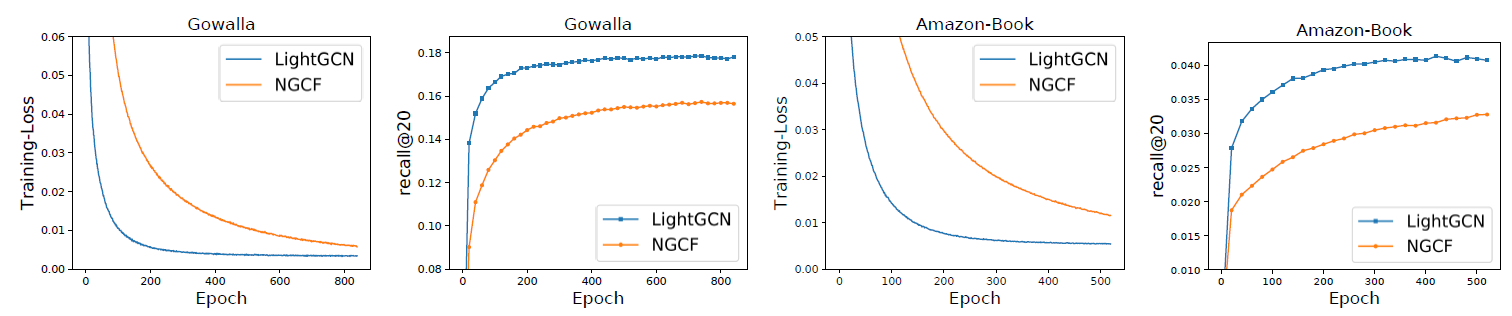
   我们在下图中进一步绘制了training loss 和 testing recall 的训练曲线（training curves），从而揭示 LightGCN 的优势，并明确训练过程。训练曲线是每隔 20 个 epoch 收集一次训练损失和测试召回率。Yelp2018 结果的趋势和 Gowalla/Amazon-Book 相同，因为篇幅有限这里忽略Yelp2018 的结果曲线。

   可以看到：

   • 在所有情况下，LightGCN 的表现都远远超过 NGCF。

     例如在 Gowalla 数据集上，NGCF 论文中报告的最高召回率为 0.1570，而我们的 LightGCN 在 4 层设置下可以达到 0.1830%，高出 16.56% 。

     平均而言，三个数据集的召回率提高了 16.52%、ndcg 提高了 16.87%，这是相当显著的提升。

   • 可以看到 LightGCN 的性能优于 NGCF-fn。NGCF-fn 是删除特征变换和非线性激活的 NGCF 变体。由于 NGCF-fn 仍然包含比 LightGCN 更多的操作（如，自连接、图卷积中 user embedding 和 item embedding 之间的交互、dropout ），这表明这些操作对于 NGCF-fn 也可能是无用的。

   • 增加层数可以提高性能，但是增益会逐渐减少。一般的观察是：将层数从 0 （即矩阵分解模型）增加到 1 会导致最大的性能增益，并且在大多数情况下使用 3层会导致令人满意的性能。这一观察结果和 NGCF 的发现一致。

   • 在训练过程中，LightGCN 始终获得较低的训练损失，这表明 LightGCN 比 NGCF 更容易拟合训练数据。此外，较低的训练损失成功地转化为更好的测试准确性（accuracy），这表明了 LightGCN 强大的泛化能力。

     相比之下，NGCF 较高的训练损失和较低的测试准确性反映了训练好如此重型heavy 的模型的实际难度。

   注意，在图中我们显示了两种方法在最佳超参数设置下的训练过程。虽然提高 NGCF 的学习率可以降低其训练损失（甚至低于 LightGCN），但是无法提高测试召回率，因为以这种方式降低训练损失只能为 NGCF 找到无效解 （trivial solution）。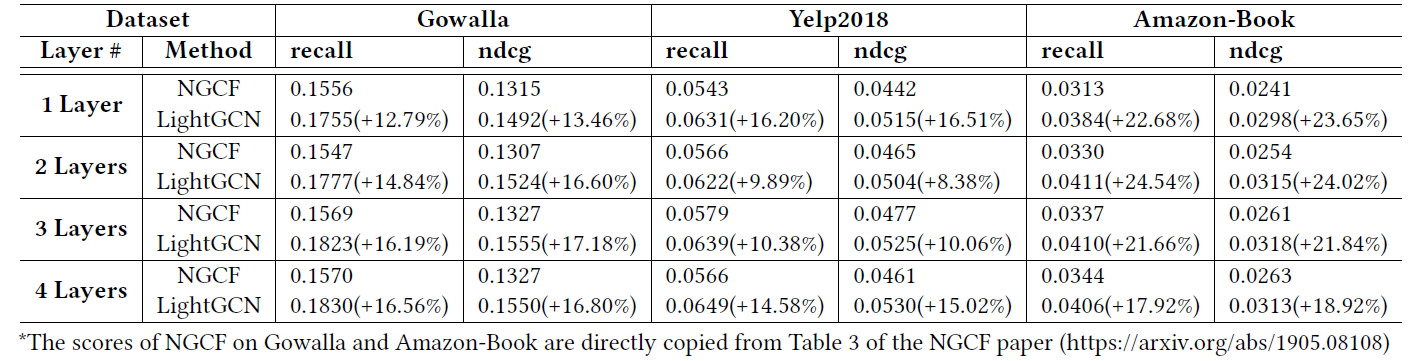

   

   

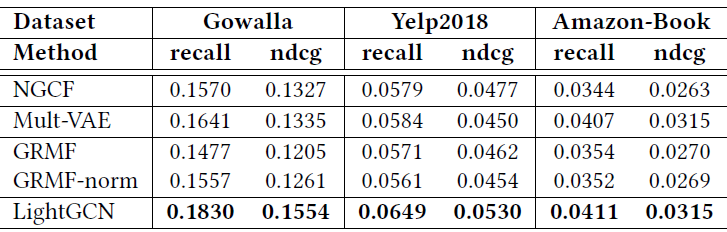
2. 和 SOA 模型的比较：下表给出了LightGCN 和其它baseline 方法的性能比较。我们展示了我们可以为每种方法获得的最佳得分。

   可以看到：

   • LightGCN 在所有三个数据集上始终优于其它方法，证明了其简单而合理的设计的有效性。

     注意：LightGCN 可以通过调整 ${\alpha }_l$$\alpha_l$ 进一步提升效果（参加后面的消融研究），而这里我们仅使用统一的 $1/(L+1)$$1/(L+1)$ 设置以免过度调优（over-tuning）。

   • 在所有 baseline 中：

     • Mult-VAE 表现出最强的性能，优于 GRMF 和 NGCF。

     • GRMF 的性能与 NGCF 相当，优于 MF，这表明使用拉普拉斯正则化器强制 embedding 平滑的效果。

     • 通过在拉普拉斯正则化器中加入归一化，GRMF-norm 在 Gowalla 上优于 GRMF、在 Yelp2018 和 Amazon-Book 上没有任何收益。

   

1.2.2 消融研究

1. 我们通过展示层组合（layer combination）和对称的 sqrt 归一化如何影响 LightGCN 的性能来进行消融研究。

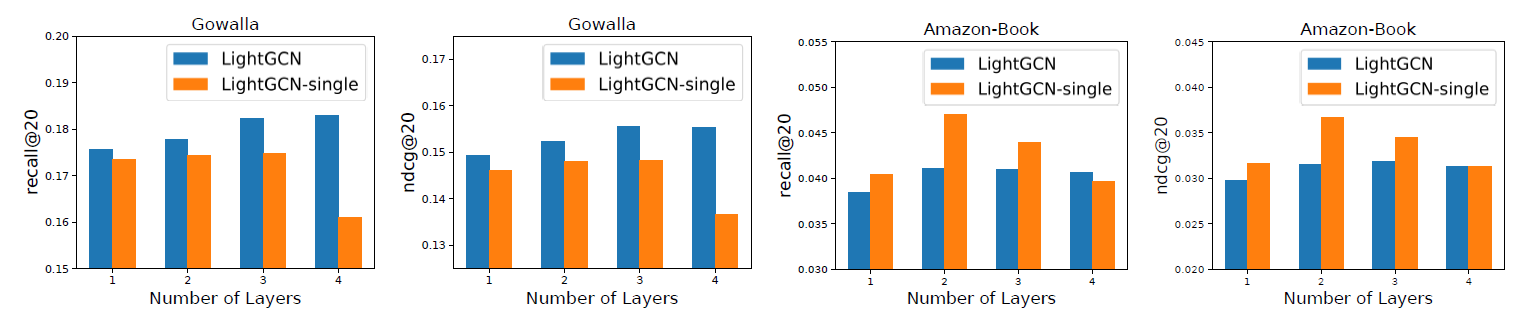
   为了证明前面分析的 LightGCN 的合理性，我们进一步研究了 embedding smoothness （这是 LightGCN 有效的关键原因）的影响。

2. 层组合的影响：下图显示了 LightGCN 及其变体 LightGCN-single 的结果。其中 LightGCN-single 不使用层组合，即仅仅将 ${\mathbf{E}}^{(L)}$$\mathbf E^{(L)}$ 用于 $L$$L$ 层 LightGCN 的最终预测。

   由于篇幅有限，我们省略了 Yelp2018 上的结果，这与 Amazon-Book 显示出类似的趋势。可以看到：

   • 聚焦 LightGCN-single，我们发现：当层数从 1 增加到 4 时，它的性能先提升然后下降；在大多数情况下，峰值点在 2 层，然后迅速下降到 4 层这个最差点。

     这一结果表明：使用一阶和二阶邻居来平滑节点的embedding 对于 CF 非常有用，而在使用高阶邻居时会遇到过度平滑的问题。

   • 聚焦 LightGCN，我们发现：它的性能随着层数的增加而逐渐提高。即使使用 4 层，LightGCN 的性能也不会下降。

     这证明了layer combination 解决过度平滑的有效性，正如我们前面技术分析中（和 APPNP 的关联）所表述的那样。

   • 比较这两种方法，我们发现： LightGCN 在 Gowalla 上的表现始终优于 LightGCN-single，但是在 Amazon-Book 和 Yelp2018 上则不然（其中2 层 LightGCN-single 表现最好）。

     对于这种现象，在得出结论之前需要注意两点：

     • LightGCN-single 是 LightGCN 的特例。如果将 ${\alpha }_L=1$$\alpha_L =1$，其它 ${\alpha }_l=0$$\alpha_l=0$，则 LightGCN 降级为 LightGCN-single 。

     • 在 LightGCN 中，我们没有调优 ${\alpha }_l$$\alpha_l$ 而是简单地将其设为 $1/(L+1)$$1/(L+1)$ 。因此我们可以看到通过调优 ${\alpha }_l$$\alpha_l$ 进一步提高 LightGCN 性能的潜力。

   

3. 对称 sqrt 归一化：在 LightGCN 中，我们在执行邻域聚合时对每个邻域 embedding 采用对称 sqrt 归一化 $\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}$$\frac{1}{\sqrt{|\mathcal N_u||\mathcal N_i|}}$ 。为了研究其合理性，我们在这里探索了三种不同的选择：

   • 仅使用左侧目标节点的系数，即左侧归一化，用 -L 来表示。

   • 仅使用右侧邻居节点的系数，即右侧归一化，用 -R 来表示。

   • 使用 L1 归一化，即移除平方根，用 -L1 来表示。

   注意，如果移除整个归一化本身，那么训练会变得数值不稳定，并且会受到 not-a-value:NAN 问题的影响，因此这里我们不会比较这个配置。

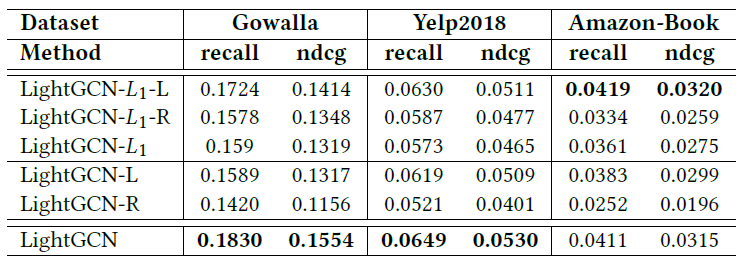
   下表给出了3 层 LightGCN 的结果， 可以看到：

   • 一般而言，最佳设置是使用对称 sqrt 归一化（即 LightGCN 的当前设计）。移除任何一侧都会大大降低性能。

   • 次优设置是仅在左侧使用 L1 归一化，即 LightGCN-L1-L，这相当于通过 in degree 将邻接矩阵归一化为随机矩阵（stochastic matrix）。

   • 两侧对称归一化有助于 sqrt 归一化（即 LightGCN vs LightGCN-L/LightGCN-R），但是会降低 L1 归一化的性能（即 LightGCN-L1 vs LightGCN-L1-L/LightGCN-L1-R）。

   

4. Embedding Smoothness 分析：正如我们在前面分析的那样，一个 2 层 LightGCN 根据用户交互 item 上重叠（overlap）的用户来平滑用户的 embedding，两个用户之间的平滑强度（smoothing strength） $c_{v\to u}$$c_{v\rightarrow u}$ 根据以下公式来衡量：

   $$c_{v\to u}=\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_v|}}\sum _{i\in {\mathcal{N}}_u\cap {\mathcal{N}}_v}\frac{1}{|{\mathcal{N}}_i|}$$

   我们推测这种 embedding 平滑是 LightGCN 有效性的关键原因。为了验证这一点，我们首先将用户 embedding 的平滑性定义为：

   $$S_U=\sum _{u=1}^M\sum _{v=1}^M{c}_{v\to u}{(\frac{{\overrightarrow{\mathbf{e}}}_u}{{\Vert {\overrightarrow{\mathbf{e}}}_u\Vert }_2}-\frac{{\overrightarrow{\mathbf{e}}}_v}{{\Vert {\overrightarrow{\mathbf{e}}}_v\Vert }_2})}^2$$

   其中 embedding 的 L2 范数用于消除 embedding 幅度（scale）的影响。

   类似地，我们可以获得 item embedding 的平滑性定义。

   理论上如果两个用户平滑强度 $c_{v\to u}$$c_{v\rightarrow u}$ 较大，则他们之间应该越相似，即 ${(\frac{{\overrightarrow{\mathbf{e}}}_u}{{\Vert {\overrightarrow{\mathbf{e}}}_u\Vert }_2}-\frac{{\overrightarrow{\mathbf{e}}}_v}{{\Vert {\overrightarrow{\mathbf{e}}}_v\Vert }_2})}^2$$\left(\frac{\mathbf{\vec e}_u}{\left\|\mathbf{\vec e}_u\right\|_2}-\frac{\mathbf{\vec e}_v}{\left\|\mathbf{\vec e}_v\right\|_2}\right)^2$ 很小。因此 $S_U$$S_U$ 可以视为一种平滑性损失（smoothness loss），该值越小那么embedding 越平滑。

   下表显式了矩阵分解（即使用 ${\mathbf{E}}^{(0)}$$\mathbf E^{(0)}$ 进行模型预测）、2 层的 LightGCN-single （即使用 ${\mathbf{E}}^{(2)}$$\mathbf E^{(2)}$ 进行模型预测）这两个模型的平滑性。注意：2 层 LightGCN-single 在推荐准确性方面远远超过 MF。

   可以看到：LightGCN-single 的平滑性损失远远低于 MF。这表明，通过进行 light graph convolution ，embedding 变得更平滑、更适合用于推荐。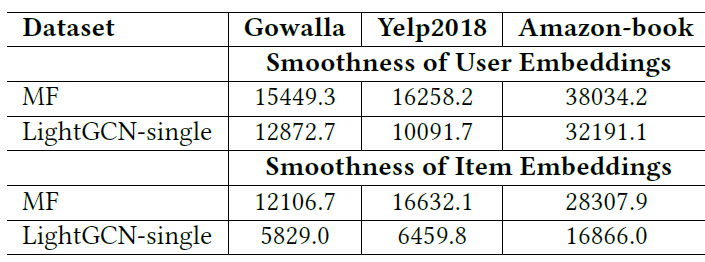

   

1.2.3 超参数研究

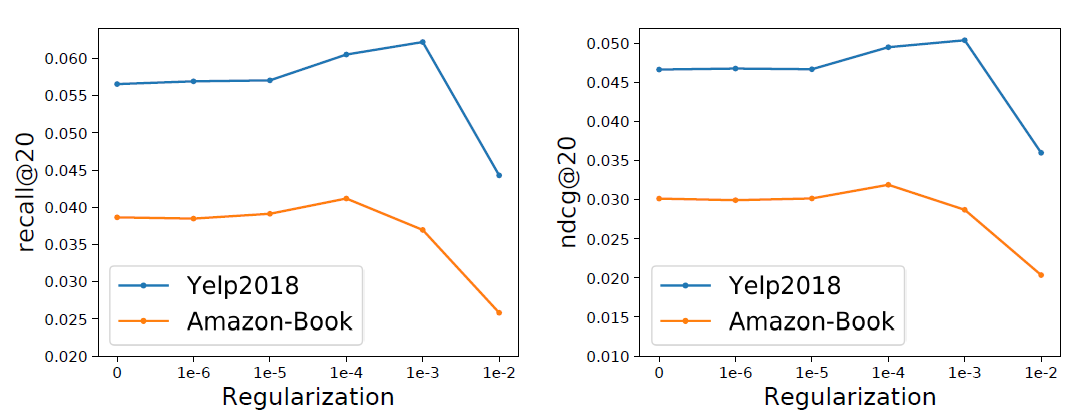
1. 当 LightGCN 应用于新数据集时，除了标准的超参数学习率之外，最重要的超参数是 L2正则化系数 $\lambda$$\lambda$ 。这里我们研究了一个 2 层的 LightGCN 的性能针对超参数 $\lambda$$\lambda$ 变化的曲线，如下图所示。可以看到：

   • LightGCN 对 $\lambda$$\lambda$ 相对不敏感。即使当 $\lambda =0$$\lambda = 0$ 时，LightGCN 也比 NGCF 要好。而 NGCF 额外使用 dropout 来防止过拟合。

     这表明 LightGCN 不太容易过拟合，因为 LightGCN 中唯一可训练的参数是第 0 层的 ID embedding，所以模型很容易训练和正则化。

   • Yelp 2018、Amazon-Book、Gowalla 数据集上，$\lambda$$\lambda$ 的最佳取值分别为 ${10}^{-3},{10}^{-4},{10}^{-4}$$10^{-3},10^{-4},10^{-4}$ 。

     当 $\lambda >{10}^{-3}$$\lambda \gt 10^{-3}$ 时，模型性能下降得很快，这表明太强的正则化将对模型正常训练产生负面影响，因此不鼓励这样做。

   

2. 我们相信 LightGCN 的洞察对推荐模型的未来发展具有启发意义。随着链接图数据 linked graph data 在实际应用中的流行，基于图的模型在推荐中变得越来越重要。通过显式地利用预测模型中实体之间的关系，基于图的模型优于传统的监督学习方案（如隐式利用实体之间关系的分解机 FM ）。

   例如，最近的一个趋势是利用辅助信息，如 item 知识图、社交网络、多媒体内容，从而进行推荐。在这个过程中，GCN 已经建立了 SOTA 技术。然而，这些模型也可能会遇到 NGCF 的类似问题，因为 user-item 交互图也由相同的、可能不必要的神经操作建模。我们未来计划在这些模型中探索 LightGCN 的思想。

   另一个未来的方向是个性化层组合权重 ${\alpha }_l$$\alpha_l$ ，以便为不同的用户启用自适应阶次的平滑。例如，稀疏用户可能需要来自高阶邻居的更多信号，而活跃用户可能只需要低阶邻居的信号。

   最后，我们将进一步探索 LightGCN 简单性的优势，研究非采样回归损失（non-sampling regression loss）是否存在快速解决方案，并将其流式传输streaming 到在线工业场景。